Question

The average age of the population of licensed drivers in a county is µ = 42.6, σ = 12, and the distribution is approximately normal. A county police officer was interested in whether the average age of drivers receiving parking tickets differed from the average age of the driving population. She obtained a sample of N = 25 drivers receiving parking tickets. The average age of these drivers was M = 40.5. Perform the appropriate hypothesis test to determine whether this group differs from the population of drivers in the county.

a. What are the hypotheses in formal statistical notation?

Answer 1

a. Hypotheses: Null Hypothesis (H0): μ (population mean) = 42.6 Alternative Hypothesis (H1): μ ≠ 42.6

b. Distribution/Rejection Region: Assuming a two-tailed test with a significance level (α), find critical values or shading regions in tails.

c. Test Statistic: z =
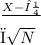`\frac{X- μ}(σ)/(√(N) )` . Substitute values: z =​
`(40.5−42.6)/((12)/(√(25) ))`

d. Decision & Results: Compare the test statistic to critical values. If in the rejection region, reject H0. Communicate findings with significance level α.

a. Hypotheses:

Null Hypothesis (H0): μ (population mean) = 42.6

Alternative Hypothesis (H1): μ ≠ 42.6

b. Distribution/Rejection Region:

Since the null hypothesis is two-tailed, we'll use a significance level (α) to find critical values.

Assuming a standard normal distribution and α = 0.05, critical values are approximately ±1.96.

Draw a normal distribution curve with these critical values marked in the tails.

| | | | | | |

-----|--------|--------|--------|--------|--------|--------|-----

-1.96 0 +1.96

c. Test Statistic: z =
`\frac{X- μ}(σ)/(√(N) )`

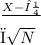
Substitute values: z =
`(40.5−42.6)/((12)/(√(25) ))` =
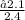`(−2.1)/(2.4)` =−0.875

Mark this value on the distribution:

| | | | | | |

-----|--------|--------|--------|--------|--------|--------|-----

-1.96 0 +1.96

-0.875

d. Decision & Results:

The test statistic (-0.875) falls within the non-rejection region between -1.96 and +1.96.

Therefore, we fail to reject the null hypothesis.

There is not enough evidence to conclude that the average age of drivers receiving parking tickets differs significantly from the average age of the driving population in the county at a 5% significance level.

Question

The average age of the population of licensed drivers in a county is µ = 42.6, σ = 12, and the distribution is approximately normal. A county police officer was interested in whether the average age of drivers receiving parking tickets differed from the average age of the driving population. She obtained a sample of N = 25 drivers receiving parking tickets. The average age of these drivers was M = 40.5. Perform the appropriate hypothesis test to determine whether this group differs from the population of drivers in the county.

a. What are the hypotheses in formal statistical notation?

b. Draw the distribution/rejection region(s)/critical value(s).

c. Compute the test statistic and show where it falls on your distribution in part b.

d. Make decision & Communicate results.