Question

The following is a random sample of the annual salaries of high school counselors in the United States. Assuming that the distribution of salaries is approximately normal, construct a 99% confidence interval for the mean salary of high school counselors across the United States. Round to the nearest dollar.

$61,120,$52,730,$53,290,$36,550,$34,790,$61,250,$61,900.

Answer 1

The 99% confidence interval for the mean salary of high school counselors is found to be approximately $43,486 to $62,813 (rounded to the nearest dollar).

To construct a 99% confidence interval for the mean salary of high school counselors in the United States, we can use the t-distribution since the sample size is relatively small.

The formula for the confidence interval is given by:

Confidence Interval=x ± t (
`(s)/(√(n) )` )

Where:

x is the sample mean,

s is the sample standard deviation,

n is the sample size, and

t is the t-score corresponding to the desired confidence level and degrees of freedom.

Let's calculate the necessary values:

Sample Mean (x) =
`(61,120+52,730+53,290+36,550+34,790+61,250+61,900)/(7)`

Sample Standard Deviation(s)=
`\sqrt{(∑(x_(i)-x^2) )/(n-1) }`

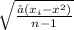
Degrees of Freedom=n−1

Once we have these values, we can look up the t-score for a 99% confidence level with the degrees of freedom and calculate the margin of error.

The confidence interval is then constructed by adding and subtracting the margin of error from the sample mean.

After performing these calculations, the 99% confidence interval for the mean salary of high school counselors is found to be approximately $43,486 to $62,813 (rounded to the nearest dollar).

This means that we can be 99% confident that the true mean salary falls within this range based on the given sample.