Question

The reading of a spring balance when a block is suspended from it in air is 60 newton. This reading is changed to 40 newton when the block is fully SUbmerged in water. The specific gravity of the block must therefore:

a. 3
b. 2
c. 6
d. 3/2

Answer 1

Answer: Specific gravity of the block = 3

Explanation:

g = gravitational acceleration

m = mass

ρ = density

W = weight = mg

W₁ = 60 N

W₂ = 40 N

ΔW = W₁ - W₂ = ρ₁Vg => V = ΔW : (ρ₁g)

ρ = m : V = W/g : [ΔW / (ρ₁g)]

ρ₁ = water density = 1 g /cm³

ρ = W ρ₁g / (gΔW ) = Wρ₁ /ΔW = 60 N /20 N x 1 g /cm³= 3 g /cm³

ρ = 3 g /cm³

specific gravity = ρ block / ρ water = 3 g /cm³ : 1 g/cm³ = 3

Answer 2

`3`.

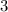Step-by-step explanation:

The specific gravity (relative density) of a material is the ratio between the density of this material and the density of water. Assuming that the density of the block in this question is uniform, the specific gravity of the block would be:

`\displaystyle (\text{specific gravity of block}) = \frac{\rho(\text{block})}{\rho(\text{water})}`.

Given the spring balance reading before and after submerging the block, the specific gravity of the block in this question can be found in the following steps:

• From the difference in the spring balance reading, find the buoyant force on the block when submerged. Deduce the weight of water that the block displaced.
• Find an expression for the density of water and for the density of the block.
• Divide the expression for the density of the block by that of the density of water to find the specific gravity of the block.

In this question, the spring balance reading is
`(60 - 40) \; {\rm N} = 20\; {\rm N}` lower when the block is submerged than when the block was in the air. This difference would be equal to the magnitude of the buoyant force on the block. In other words:

`(\text{buoyant force}) = 20\; {\rm N}`.

The buoyant force on this block is equal to the weight of the liquid that the block has displaced. Let
`V(\text{block})` denote the volume of the block, and let
`g` denote the gravitational field strength. Since the block is fully submerged in water, the volume of the water displaced would be equal to the volume of the block:

`V(\text{water displaced}) = V(\text{block})`.

`\begin{aligned} m(\text{water displaced}) &= \rho(\text{water})\, V(\text{water displaced}) \\ &= \rho(\text{water})\, V(\text{block})\end{aligned}`.

Therefore:

`\begin{aligned} (\text{buoyant force}) &= (\text{weight of water displaced}) \\ &= m(\text{water displaced})\, g \\ &= \rho(\text{water})\, V(\text{block})\, g\end{aligned}`.

Rearrange this equation to obtain an expression for
`\rho(\text{water})`:

`\displaystyle \rho(\text{water}) = \frac{(\text{buoyant force})}{V(\text{block})\, g}`.

Assuming that the density of the block is uniform, derive a similar expression for the density of the block:

`\displaystyle \rho(\text{block}) = \frac{(\text{weight})}{V(\text{block})\, g}`.

To find the specific gravity of the material of the block, divide the density of the block by the density of water:

`\begin{aligned} \frac{\rho(\text{block})}{\rho(\text{water})} &= \frac{\displaystyle \frac{(\text{weight})}{V(\text{block})\, g}}{\displaystyle \frac{(\text{buoyant force})}{V(\text{block})\, g}} \\ &= \frac{(\text{weight})}{(\text{buoyant force})} \\ &= \frac{60\; {\rm N}}{20\; {\rm N}} \\ &= 3\end{aligned}`.

In other words, the specific gravity of the block would be
`(60\; \rm N}) / (20\; {\rm N}) = 3`.