Question

When the rms voltages VL, Vc and VR are measured respectively across the inductor L, the capacitor C and the resistor R in a series LCR circuit connected to an AC source, it is found that the ratio VL : Vc: Vr=1:2:3. If the rms voltage of the AC source is 100 V, then VR is close to

(a.) 50 V
(b.) 70 V
(c.) 90 V
(d.) 100 V

Answer 1

VR is close to 90 V. Hence the correct option is c.

In a series LCR circuit connected to an AC source, the voltage across each component is influenced by the impedance of the component and the phase relationship within the circuit. The given ratio VL:VC:VR=1:2:3 suggests that the voltage across the capacitor (VC) is twice that of the inductor (VL), and the voltage across the resistor (VR) is three times that of the inductor.

In AC circuits, the voltage across an impedance (V=I⋅Z) is determined by the current (I) flowing through it and its impedance (Z). The impedance for a resistor (ZR​) is simply the resistance (R), for an inductor (ZL) it is jωL (where j is the imaginary unit, ω is the angular frequency, and L is the inductance), and for a capacitor (ZC​) it is 1/jωC (where C is the capacitance).

Given the ratio and knowing that the total rms voltage of the AC source is 100 V, we can express the voltages across each component as multiples of a variable, say x. Let VL=x, VC=2x, and VR=3x. The total voltage is the phasor sum of individual voltages:
`V_t_o_t_a_l=√(VL^2+VC^2+VR^2)`

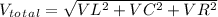
By solving for x and subsequently calculating VR, we find VR≈90 V. Thus, the rms voltage across the resistor is approximately 90 V. Hence the correct option is c.