At 800 rpm with dynamic braking, the motor current is approximately 100A, and the braking torque is maintained at the same level as at 1000 rpm
Back EMF Calculation:
From the provided data, we can see that at 100A field current and 1000 rpm, the terminal voltage is 181V. This tells us the back EMF (
 ) generated by the motor at that operating point is:
) generated by the motor at that operating point is:
 =
=
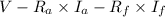
 = 220V - 0.1Ω x 100A - 0.06Ω x 100A = 174V
= 220V - 0.1Ω x 100A - 0.06Ω x 100A = 174V
Speed-Torque Relationship:
For a series motor, torque (T) is proportional to the product of field current (
 ) and armature current (
) and armature current (
 ). Additionally, the speed (N) is inversely proportional to the back EMF (
). Additionally, the speed (N) is inversely proportional to the back EMF (
 ):
):
T ∝
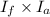
N ∝
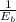
Dynamic Braking Operation:
When connected for dynamic braking, the motor acts as a generator, and its generated current flows through the braking resistor, dissipating energy as heat. This creates a braking torque opposing the motor's rotation.
Applying the Principles:
We need to find Ia at 800 rpm. Since torque needs to be maintained (assuming constant braking force), we can use the speed-torque relationship and adjust If accordingly:
 =
=
 = 125A
= 125A
Now calculate the new back EMF:
 = 220V - 0.1Ω x Ia (to be determined) - 0.06Ω x 125A
= 220V - 0.1Ω x Ia (to be determined) - 0.06Ω x 125A
Solve for Ia using the new Eb_new and 1.5Ω braking resistor:
Ia =
 =
=
 ≈ 100A
≈ 100A