Question

A toy is in the shape of a solid cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 21 cm and 40 cm respectively, and the height of cone is 15 cm, then find the total surface area of the toy. [π = 3.14, be taken]

Answer 1

The total surface area of the toy is 3390 cm².

The total surface area of the toy, which is a combination of a solid cylinder surmounted by a conical top, can be calculated by finding the sum of the lateral surface areas of the cylinder and the cone, along with the base areas of both.

Surface area of the cylindrical part:

The lateral surface area (excluding the top and bottom) of a cylinder is given by 2πrh, where r is the radius and h is the height. In this case, the radius (r) is half of the diameter, so r= 40/2=20 cm. The height (h) of the cylindrical part is 21 cm. Therefore, the surface area of the cylindrical part is 2π×20×21 cm².

Surface area of the conical part:

The lateral surface area of a cone is given by πrl, where r is the radius of the base and l is the slant height. The radius of the conical part is the same as the radius of the cylindrical part, 20 cm. To find the slant height (l), we can use the Pythagorean theorem:

l=
`√(r^2+h^2)`. The height (h) of the conical part is 15 cm. Therefore, the slant height l is
`\sqrt{20^2+15^2`cm. The surface area of the conical part is

π×20×
`√(20^2+15^2)`cm².

Base areas:

The base area of the cylinder is πr^2, and the base area of the cone is πr^2. Therefore, the total base area is 2πr^2.

Total surface area:

Adding the surface areas of the cylindrical and conical parts, along with the base areas, gives the total surface area of the toy:

Total Surface Area=2πrh+πr
`√(r^2+h^2) +2\pi r^2`

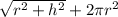
Substituting the given values, the total surface area is:

2π×20×21+π×20×
`√(20^2+15^2)` +2π×20^2

Calculating this expression yields the total surface area of the toy as 3390 cm².