Question

A stone is dropped into a well and the sound of impact of stone with the water is heard after 2.056 s of the release of stone from the top. If the acceleration due to gravity is 980 cms⁻²and the velocity of sound in air is 350 ms⁻¹, then the depth of the well is

A 7 m
B 19.6 m
C 700 m
D 1960 m

Answer 1

The depth of the well is 1960 m. Hence the correct option is d.

To determine the depth of the well, we can use the equation for the total distance traveled by the stone during its fall. The total distance consists of two parts: the distance covered by the stone in free fall and the distance covered by the sound wave traveling back up.

Distance covered in free fall:

The distance covered by the stone in free fall can be described by the equation s=ut+ 1/2gt^2, where u is the initial velocity (which is zero in this case since the stone is dropped), g is the acceleration due to gravity (given as 980 cm/s²), and t is the time of fall. Since the stone is dropped, the initial velocity term becomes zero, simplifying the equation to s1​=1/2gt^2.

Distance covered by sound wave:

The sound wave travels back up, and its distance is given by s2​=vt, where v is the velocity of sound in air (given as 350 m/s) and t is the time taken for the sound to travel back up.

Total distance:

The total distance s is the sum of s1​ and s2​, given by s=s1​+s2​. Substituting the expressions for s1​ and s2​ and solving for t, we get

t=
`s/v+√(v^2+2gs)`.

Given data and calculation:

The total time t is given as 2.056 seconds. Substituting the known values, we can solve for s, the depth of the well.

2.056=
`s/350+ √(350^2+2*980*s)`

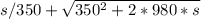
Solving this equation gives s≈1960 meters.

Therefore, the correct answer is option D: 1960 m, representing the depth of the well. Hence the correct option is d.