Question

A soccer ball is kicked from the ground with an initial vertical velocity of 19.6 meters per second. Its height is modeled by the function h(t) = -4.9t² + 19.6t. What is the maximum height reached by the soccer ball?

1) 9.8 meters
2) 19.6 meters
3) 39.2 meters
4) 49 meters

Answer 1

To find the maximum height reached by the soccer ball, calculate the time at the vertex of the parabolic height function and substitute back into the function. The soccer ball reaches a maximum height of 19.6 meters.

Step-by-step explanation:

The maximum height reached by a soccer ball kicked with a vertical velocity can be found using the vertex of the parabolic equation representing its height over time. Given the height function h(t) = -4.9t² + 19.6t, we want to find the time at which the maximum height is reached. This occurs when the derivative of the height function with respect to time is zero. By calculating the derivative and setting it to zero, we can solve for the time t at the vertex of the parabola, which is t = -b/(2a). Using the given coefficients a = -4.9 and b = 19.6, we find that the time at the vertex is
`t = 19.6/(2*4.9) = 2 seconds`.

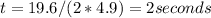Now we can substitute this time back into the original height function to find the maximum height:
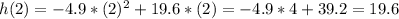`h(2) = -4.9*(2)^2 + 19.6*(2) = -4.9*4 + 39.2 = 19.6` meters. Thus, the maximum height reached by the ball is 19.6 meters.