Question

Drag the tiles to the correct boxes to complete the pairs. Match each rational expression to its simplest form.

Answer 1

The rational expressions matched to their simplest forms are:

(x² - 4) / (x² - 2x - 8) = (x + 2) / (x - 4)

(3x² + 6x) / (3x² - 12) = (x + 2) / (x - 4)

(5x² - 25x) / (20x² - 5) = (x - 5) / (4x + 1)

Step-by-step explanation:

In the first rational expression, we factorize the numerator and denominator to get (x + 2)(x - 2) / (x + 2)(x - 4). We then cancel out the common factor of (x + 2), leaving us with the simplest form of (x - 2) / (x - 4).

For the second expression, we factor out a common factor of 3x from the numerator and denominator, resulting in (3x(x + 2)) / (3(x² - 4)). We simplify further by canceling out the common factor of 3, giving us the simplest form of (x + 2) / (x - 4).

Lastly, in the third expression, we factor out a common factor of 5x from the numerator and a common factor of 5 from the denominator, leading to x(x - 5) / 5(4x + 1). This simplifies to the simplest form of (x - 5) / (4x + 1).

These simplifications are achieved through factoring and canceling out common factors, resulting in the expressions being represented in their simplest forms.

Complete Question:

Given the rational expressions matched to their simplest forms:

1.
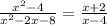
`\((x^2 - 4)/(x^2 - 2x - 8) = (x + 2)/(x - 4)\)`

2.
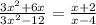
`\((3x^2 + 6x)/(3x^2 - 12) = (x + 2)/(x - 4)\)`

3.
`\((5x^2 - 25x)/(20x^2 - 5) = (x - 5)/(4x + 1)\)`

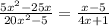
Explain the simplification process for each expression, including the factoring steps and the cancellation of common factors. Illustrate how the original expressions are transformed into their simplest forms.