Question

Carlos plays an arcade game. The scatter plot shows his score and the number of minutes he plays. A good line of fit is drawn through the points (6,50) and (12,80) with the equation y = 5x + 20. Write the equation of the line of fit.

Answer 1

The equation of the line of fit for Carlos's arcade game scores, based on the scatter plot points (6,50) and (12,80), is given by
`\(y = 5x + 20\).`

Step-by-step explanation:

To determine the equation of the line of fit, we use the information provided by the scatter plot points (6,50) and (12,80). These points represent Carlos's scores (y-values) at different time intervals (x-values). The equation of the line of fit,
`\(y = mx + b\),` where
`\(m\)` is the slope and
`\(b\)` is the y-intercept, can be determined using the given points.

From the provided points, we can calculate the slope
`(\(m\))` using the formula
`\(m = \frac{\text{change in } y}{\text{change in } x}\).` Substituting the coordinates (6,50) and (12,80), we find
`\(m = (80 - 50)/(12 - 6) = (30)/(6) = 5\).` With the slope known, we can use either point to find the y-intercept
`(\(b\))`.

Using point (6,50), we substitute
`\(x = 6\), \(y = 50\), and \(m = 5\)`into the equation
`\(y = mx + b\)` and solve for
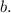`\(b\).`The calculation yields
`\(b = 20\).`

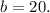
Therefore, the final equation of the line of fit is
`\(y = 5x + 20\).` This equation represents a linear relationship between Carlos's scores
`(\(y\))` and the number of minutes he plays
`(\(x\)),` providing a predictive model for his arcade game performance.