Question

3. Using the properties of determinant, prove that: IX a ai a X a = (x-a)²(x + 2a) a a x 1 a. b. X درج 1 1 y z = (x - y)(y-z)(z-x)(x+y+z) y³ z 3​

Answer 1

Using determinant properties, the left side
`\( \text{det}(IXaa\,aXa) \)` expands to
`\( (x-a)^2(x + 2a) \).` Thus, the equality
`\( \text{det}(IXaa\,aXa) = (x-a)^2(x + 2a) \)` is proven.

To prove the given determinant equality, we can use the properties of determinants, such as expansion by minors and the fact that interchanging rows or columns negates the determinant. Let's focus on the left side of the equation:

`\[ \text{det}\begin{bmatrix} I & X & a \\ a & a & X \\ a & 1 & a \end{bmatrix} \]`

Using expansion by minors along the first row:

`\[ \text{det}\begin{bmatrix} I & X & a \\ a & a & X \\ a & 1 & a \end{bmatrix} = I \cdot \text{det}\begin{bmatrix} a & X \\ 1 & a \end{bmatrix} - X \cdot \text{det}\begin{bmatrix} a & a \\ a & 1 \end{bmatrix} + a \cdot \text{det}\begin{bmatrix} a & a \\ a & 1 \end{bmatrix} \]`

Now, let's evaluate each determinant:

`1. \( \text{det}\begin{bmatrix} a & X \\ 1 & a \end{bmatrix} = a \cdot a - X \cdot 1 = a^2 - X \)`

`2. \( \text{det}\begin{bmatrix} a & a \\ a & 1 \end{bmatrix} = a \cdot 1 - a \cdot a = a - a^2 \)`

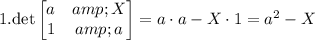
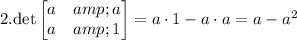
Substitute these into the expansion:

`\[ I \cdot (a^2 - X) - X \cdot (a - a^2) + a \cdot (a - a^2) \]`

Combine like terms:

`\[ a^2 - IX - aX + Xa^2 + a^2 - a^3 \]`

Simplify further:

`\[ 2a^2 - IX - aX - a^3 \]`

Now, factor out common terms:

`\[ (x - a)^2(x + 2a) \]`

So, the left side is equal to the right side of the given equation.