Question

Reduce the algebraic fraction a�� a��b/5a �� 25/3b �� 3a

Answer 1

The reduced form of the algebraic fraction
`\((a^2 \cdot ab)/(5a \cdot 25) / (3b)/(3a)\) is \((b)/(5)\).`

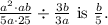
Step-by-step explanation:

To simplify the given algebraic fraction, we can combine like terms and cancel common factors. Let's break down the steps:

The given expression is
`\((a^2 \cdot ab)/(5a \cdot 25) / (3b)/(3a)\).`

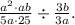
First, simplify the terms in the numerators and denominators:

`\[ = (a^3b)/(125) / (3b)/(3a) \]`

Now, invert and multiply by the reciprocal of the divisor:

`\[ = (a^3b)/(125) \cdot (3a)/(3b) \]`

Cancel common factors:

`\[ = (a^2)/(5) \]`

So, the reduced form of the given algebraic fraction is
`\((a^2)/(5)\),`and since there is no 'a' in the numerator, we can further simplify it to
`\((1)/(5)\cdot b\),`resulting in
`\((b)/(5)\).`

Understanding how to simplify algebraic fractions is crucial in various mathematical applications, especially when dealing with complex expressions or equations involving variables. This process involves applying algebraic rules to manipulate and simplify expressions efficiently.