Final answer:
The magnitude of the total acceleration of a point at the tip of the centrifuge at t=29.0s is 571.4 m/s². This acceleration is a combination of the centripetal acceleration and the tangential acceleration due to the centrifuge's deceleration. The direction is towards the center and clockwise due to the centripetal and tangential components, respectively.
Step-by-step explanation:
To calculate the magnitude of the total acceleration of a point at the tip of the centrifuge at t=29.0s, we need to consider both the centripetal acceleration and the tangential acceleration at that instant. The centrifuge decelerates from 10,000 revolutions per minute (rpm) to rest in 30 seconds with constant angular acceleration.
First, we convert the maximum rotation rate from rpm to radians per second (rad/s):
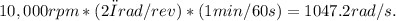
Next, we calculate the constant angular acceleration (α) using α = (ω_f - ω_i) / t, where ω_f is the final angular velocity (0 rad/s) and ω_i is the initial angular velocity (1047.2 rad/s):
α = (0 - 1047.2 rad/s) / 30 s = -34.9 rad/s².
At t = 29.0s, the angular velocity (ω) is ω = ω_i + αt = 1047.2 rad/s + (-34.9 rad/s²)(29.0s) = 53.5 rad/s.
The centripetal acceleration (ac) can be found using ac = ω²r, and the tangential acceleration (at) is given by at = αr.
Thus, ac = (53.5 rad/s)²(0.20 m) = 571.2 m/s², and at = (-34.9 rad/s²)(0.20 m) = -7.0 m/s².
Using Pythagoras' theorem, the magnitude of the total acceleration (a) is √(571.2 m/s²)² + (-7.0 m/s²)² = 571.4 m/s².
The direction of the total acceleration vector combines the direction of the centripetal acceleration (always pointing towards the center of the circular path) and the tangential acceleration (pointing in the opposite direction of rotation since the centrifuge is slowing down, thus clockwise).