Question

You are working in cooperation with the Public Health department to design an electrostatic trap for particles from auto emissions. In order to verify the correct operation of the trap the design engineers must be able to monitor the speed of the particles before they are trapped. If the particles are moving too fast then they cannot be effectively trapped. The particular detector the engineers want to use is only sensitive to particles moving less than 1000 m/s.The following design parameters are given.

The average emission particle that enters the device is ionized by exposure to ultraviolet radiation resulting in the removal of electrons so that it has a charge of +3.0 x 10-8 C.
The trapping element is a single large square plate negatively charged with a charge density of -8.0 x 10-6 C/m2.
The average particle in the emission stream is moving 900 m/s when it is 15 cm from the plate.
The detector for the particles is located 7.0 cm from the plate.
An average emission particle has a mass of 6.0 x 10-9 kg.

Does this electrostatic trap meets the design parameters?

Answer 1

Step-by-step explanation:

Given that:

Charge (q) on the particle = 3 × 10⁻⁸ C

mass (m) of the particle = 6 × 10⁻⁹ kg

at a distance x = 15 cm , the velocity in the plate = 900 m/s²

For the square plate, the surface charged density σ = -8 × 10⁻⁶ C/m²

To start with calculating the electric field as a result of the square plate; we use the formula;

`E = (\sigma )/(2 \varepsilon_o)`

`E = (8 * 10^(-6) )/(2 * 8.85 * 10^(-12))`

`E = 4.51977 * 10^5 \ V/m`

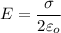
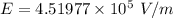
On the square plate; The electric force F = Eq

`F = (4.51977 * 10^5 \ V/m )(3* 10^(-8) \ C)`

`F = 1.3559 * 10^(-2) \ N`

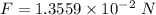
The acceleration
`a =( F)/(m){`

`a = (1.3559* 10^(-2) \ N)/(6 * 10^(-9) \ Kg)`

`a = 2.25988 * 10^6 \ m/s^2`

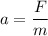
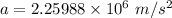
For the particle, the velocity at distance x = 7 m can be calculated by using the formula:

`((1)/(2)) mv^2 = \Delta Vq`

`v^2 = (2 Eq)/(dm)`

`v^2 = (2 * 4.51977 * 10^5 * 3 * 10^(-8) )/(0.07 * 6* 10^(-9) )`

`v^2 = 64568142.86 \ m/s`

`v =√( 64568142.86 \ m/s)`

`\mathbf{v = 8.035 * 10^3 \ m/s}`

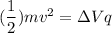
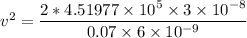
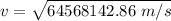
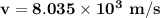
From the calculation, we realize that the charge acting between the particle and the plate is said to be "opposite".

Hence, the force is an attractive force.

Similarly, there is a gradual increase exhibited by the velocity of the particle.

Therefore, the particles get to the detector, but the detector failed to get detect due to the velocity which is greater than 1000 m/s.