Question

An arithmetic sequence has a recursive formula of an = an-1 2; a1 = 3. Part a: Choose the correct explicit formula for the arithmetic sequence above.

1) an = 3 * 2��������������
2) an = 3 * 2���
3) an = 3 * 2��������������
4) an = 3 * 2��������������

Answer 1

The correct explicit formula for the given arithmetic sequence is:

`[ an = 3 * 2^(n-1) \]`. Thus the correct option is 3)
`[ an = 3 * 2^(n-1) \]`

Step-by-step explanation:

In the given recursive formula for an arithmetic sequence,
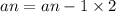`\( an = an-1 * 2 \)` with
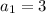`\( a_1 = 3 \)`, we can deduce the pattern by observing the common ratio. The sequence is multiplied by 2 in each step. To find the explicit formula, we need to express the nth term directly in terms of n.

Let's derive the explicit formula:

`\[ a_1 = 3 \]`

`\[ a_2 = a_1 * 2 = 3 * 2^1 \]`

`\[ a_3 = a_2 * 2 = 3 * 2^1 * 2^1 = 3 * 2^2 \]`

We can see that the exponent of 2 is one less than the term number (n). So, the explicit formula is
`\( an = 3 * 2^(n-1) \)`.

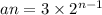This formula ensures that each term in the sequence is obtained by multiplying the first term (a1) by 2 raised to the power of (n-1), maintaining the arithmetic progression. Therefore, the correct option is
`\( \boxed{\text{3) } an = 3 * 2^(n-1)} \).`