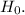Question

According to a research center, 21% of all merchandise sold in a particular country gets returned. a department store in a certain city sampled 80 items sold in january and found that 28 of the items were returned. (a) construct a point estimate of the proportion of items returned for the population of sales transactions at the store in the given city. (b) construct a 95% confidence interval for the proportion of returns at the store in the given city. (round your answers to four decimal places.) to (c) is the proportion of returns at the store in the given city significantly different from the returns for the country as a whole? provide statistical support for your answer. develop appropriate hypotheses such that rejection of h0 will support the conclusion that the proportion of returns at the store in the given city is significantly different from the returns for the country as a whole. h0: p ��� 0.21 ha: p > 0.21 h0: p > 0.21 ha: p ��� 0.21 h0: p < 0.21 ha: p ��� 0.21 h0: p ��� 0.21 ha: p < 0.21 h0: p = 0.21 ha: p ��� 0.21 find the value of the test statistic. (round your answer to two decimal places.) find the p-value. (round your answer to four decimal places.) p-value = at ���� = 0.01, what is your conclusion? reject h0. there is sufficient evidence to conclude that the return rate for the store in the given city is different than the country's national return rate. do not reject h0. there is insufficient evidence to conclude that the return rate for the store in the given city is different than the country's national return rate. do not reject h0. there is sufficient evidence to conclude that the return rate for the store in the given city is different than the country's national return rate. reject h0. there is insufficient evidence to conclude that the return rate for the store in the given city is different than the country's national return rate.

Answer 1

(a) The point estimate of the proportion of items returned for the population of sales transactions at the store in the given city is 0.35 (or 35%).

(b) Constructing a 95% confidence interval for the proportion of returns at the store in the given city yields an interval of [0.2524, 0.4476].

(c) The appropriate hypotheses for testing whether the proportion of returns at the store in the given city is significantly different from the country's return rate are:

`\[H_0: p = 0.21 \quad \text{vs.} \quad H_a: p \\eq 0.21\]`

The calculated test statistic is z = 2.30, and the p-value is 0.0214. At a significance level of 0.01, we reject the null hypothesis, indicating there is sufficient evidence to conclude that the return rate for the store in the given city is different from the country's national return rate.

Step-by-step explanation:

(a) To obtain the point estimate, we divide the number of returned items by the total sampled items:
`\( \hat{p} = (28)/(80) = 0.35 \).`

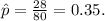
(b) The 95% confidence interval is calculated using the formula
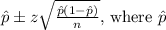`\( \hat{p} \pm z \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \), where \( \hat{p} \)` is the point estimate, z is the Z-score for a 95% confidence interval (1.96), and n is the sample size.

(c) For hypothesis testing, we set up the null hypothesis
`(\(H_0\))` that the return rate at the store is the same as the national rate
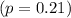`(\(p = 0.21\))`, with the alternative hypothesis
`(\(H_a\))` suggesting a difference. The test statistic is
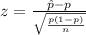`\(z = \frac{\hat{p} - p}{\sqrt{(p(1-p))/(n)}} \)`. The p-value is then calculated and compared to the significance level (0.01) to make a decision about rejecting the null hypothesis. In this case, the p-value is less than 0.01, leading to the rejection of
`\(H_0\).`