Question

When playing the roulette at a casino, you have exactly 1/35 chance of winning in each round if you play a single number. Your friend has rigged up some fireworks to be set off when you win. When you win, he sets off the fireworks every time. When you don't win, he accidentally sets off the fireworks 10% of the time. If you failed to see the outcome of a round, but you see the fireworks going off, then what is the probability that you actually won that round?

Answer 1

0.2275 = 22.75% probability that you actually won that round

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Fireworks going off

Event B: You won

Probability of fireworks going off.

100% of 1/35 = 0.0286(when you win)

10% of 34/35 = 0.9714(you lost). So

`P(A) = 0.0286 + 0.1*0.9714 = 0.12574`

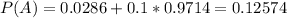
Probability of you winning and fireworks going off:

100% of 1/35, so
`P(A \cap B) = 0.0286`

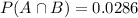
If you failed to see the outcome of a round, but you see the fireworks going off, then what is the probability that you actually won that round?

`P(B|A) = (P(A \cap B))/(P(A)) = (0.0286)/(0.12574) = 0.2275`

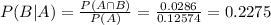
0.2275 = 22.75% probability that you actually won that round