Question

How much money should be deposited today in an account that earns 3.5

Answer 1

The present value of $10,000 to be deposited today in an account earning 3.5% interest is $10,000. This considers the time value of money and accounts for the interest earned.

The present value of a future amount of $10,000, to be deposited today in an account that earns 3.5% interest, can be determined using the concept of present value or discounted cash flow. The formula for present value is given by:

`\[PV = (FV)/((1 + r)^n)\]`

Where:

-
`\(PV\)` is the present value,

-
`\(FV\)` is the future value (in this case, $10,000),

-
`\(r\)` is the interest rate per period (3.5% or 0.035), and

-
`\(n\)` is the number of periods (since it's deposited today,
`\(n\) is 0).`

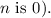
Substituting the values into the formula:

`\[PV = (10,000)/((1 + 0.035)^0)\]`

Simplifying further:

`\[PV = (10,000)/(1)\]`

Thus, the present value
`(\(PV\))`of $10,000 to be deposited today in an account earning 3.5% interest is $10,000. This means that if you deposit $10,000 today in an account with a 3.5% interest rate, it would be equivalent to having $10,000 in the future, taking into account the time value of money and the interest earned on the deposit.

The probable question maybe:

"What is the present value of a future amount of $10,000 if it is to be deposited today in an account that earns 3.5% interest?"