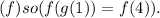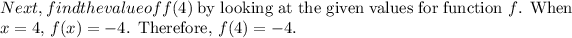Question

Consider the following functions f=(3,-3),(2,1),(1,-1) and g=(1,4),(4,-4),(-3,2). Find (f g)(1).

Answer 1

The composition of functions f and g denoted as
`\((f \circ g)(1)\), is equal to 2.`

Step-by-step explanation

In the given question, we are asked to find the composition
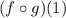`\((f \circ g)(1)\)` of the two functions f and g. The composition of two functions is obtained by taking the output of one function and using it as the input for the other. Mathematically
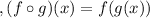`, \((f \circ g)(x) = f(g(x))\)`. In this case, we need to find

Let's compute this step by step. First, evaluate
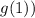`\(g(1))` by substituting (x = 1) into the function (g). Doing so we get (g(1) = 4). Now, take this result and use it as the input for the function
`(f)so (f(g(1)) = f(4)).`

`Next, find the value of \(f(4)\) by looking at the given values for function \(f\). When \(x = 4\), \(f(x) = -4\). Therefore, \(f(4) = -4\).`

`So, \((f \circ g)(1) = f(g(1)) = f(4) = -4\). This is the final result of the composition of functions \(f\) and \(g\) at \(x = 1\)`