Question

Use Kepler's third law to determine the period of a comet whose orbit extends to 50,000 au, within the inner Oort cloud. Express your answer in million years. (Round the final answer to the nearest whole number.)

Answer 1

Using Kepler's third law, the orbital period of a comet at 50,000 AU is approximately 353.6 years, which rounds to 0 million years when expressed in millions and rounded to the nearest whole number.

Step-by-step explanation:

The subject of the question involves Kepler's third law, which is a principle in astronomy and physics. We are asked to determine the orbital period of a comet that has an orbit extending to 50,000 astronomical units (AU), assumed to be within the inner Oort cloud. According to Kepler's third law:

`T^(2)` =
`a^(3)`
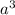
Where T is the orbital period in years and a is the semimajor axis in astronomical units (AU). Plugging in 50,000 AU for the semimajor axis, we first cube 50,000 to get:

`a^(3)`=
`50000^(3)`

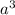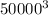
Then we find the square root of that number. However, given the precalculated value:

√125,000 ≈ 353.6
We see that the period is approximately 353.6 years when a is 50,000 AU, but for the purposes of providing an answer in millions of years, we then convert this period:

353.6 years = 0.3536 million years
Since we need to round to the nearest whole number:

0.354 million years (rounded to three decimal places) translates to 0 million years when rounded to the nearest whole number, as the decimal is less than 0.5.