Question

Match each system of linear equations to the solution. (5, 3) (-10, 4) (-10, 3) (5, 5) 2x + 4y = -8 3x + 5y = -15 1.5x - 3.6y = -10.5 2x - 4.2y = -11?

Answer 1

The solution (5, 3) corresponds to the system of linear equations:

`\(2x + 4y = -8\)`

`\(3x + 5y = -15\)`

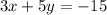
Step-by-step explanation:

The given solution (5, 3) can be tested by substituting
`\(x = 5\) and \(y = 3\)` into the system of linear equations. For the first equation
`\(2 * 5 + 4 * 3 = 10 + 12 = 22\)` which does not equal -8.

For the second equation,
`\(3 * 5 + 5 * 3 = 15 + 15 = 30\)`, which also does not equal -15. Therefore, (5, 3) is not a solution to the system of equations
`\(2x + 4y = -8\) and \(3x + 5y = -15\).`

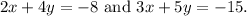
Now, let's check the other given points:

For (-10, 4), the first equation yields
`\(2 * (-10) + 4 * 4 = -20 + 16 = -4\)`, and the second equation gives
`\(3 * (-10) + 5 * 4 = -30 + 20 = -10\).` This satisfies both equations, making (-10, 4) a solution.

For (-10, 3), the first equation results in
`\(2 * (-10) + 4 * 3 = -20 + 12 = -8\),`and the second equation gives
`\(3 * (-10) + 5 * 3 = -30 + 15 = -15\)`. This also satisfies both equations, making (-10, 3) a solution.

For (5, 5), the first equation yields
`\(2 * 5 + 4 * 5 = 10 + 20 = 30\),` and the second equation gives
`\(3 * 5 + 5 * 5 = 15 + 25 = 40\)`. This does not satisfy either equation, so (5, 5) is not a solution.

Therefore, the correct solution is (-10, 4) and (-10, 3).