Question

How many ways are there to place 3 indistinguishable red chips, 3 indistinguishable blue chips, and 3 indistinguishable green chips in the squares of a 3 x 3 grid so that no two chips of the same color are directly adjacent to each other, either vertically or horizontally?

A. 12,
B. 18,
C. 24,
D. 30 ,
E. 36

Answer 1

E. 36

Explanation:

Let:

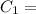`C_1 =` color 1

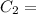`C_2 =` color 2

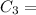`C_3 =` color 3

Case I

C₂ C₃ C₂

C₃ C₁ C₃

C₁ C₂ C₁

Since C₁ has 3 choices, then C₂ has 2 choices and C₁ has 1 choice

number of combinations = 3 × 2 × 1 = 6

Case II

C₂ C₃ C₁

C₃ C₁ C₂

C₂ C₃ C₁

Since C₁ has 3 choices, then C₂ has 2 choices and C₁ has 1 choice

number of combinations = 3 × 2 × 1 = 6

Case III

C₁ C₃ C₂

C₂ C₁ C₃

C₃ C₂ C₁

Since C₁ has 3 choices, then C₂ has 2 choices and C₁ has 1 choice

number of combinations = 3 × 2 × 1 = 6

Case IV

C₂ C₃ C₁

C₃ C₁ C₂

C₁ C₂ C₃

Since C₁ has 3 choices, then C₂ has 2 choices and C₁ has 1 choice

number of combinations = 3 × 2 × 1 = 6

Case V

C₁ C₂ C₁

C₃ C₁ C₃

C₂ C₃ C₂

Since C₁ has 3 choices, then C₂ has 2 choices and C₁ has 1 choice

number of combinations = 3 × 2 × 1 = 6

Case VI

C₁ C₂ C₃

C₃ C₁ C₂

C₁ C₂ C₃

Since C₁ has 3 choices, then C₂ has 2 choices and C₁ has 1 choice

number of combinations = 3 × 2 × 1 = 6

Therefore, the total combinations = 6 + 6 + 6 + 6 + 6 + 6

= 36