Question

An electronics hobbyist has three electronic parts cabinets with two drawers each.

One cabinet has NPN transistors in each drawer, while a second cabinet has PNP transistors in each drawer. The third cabinet has NPN transistors in one drawer and PNP transistors in the other drawer. The hobbyist selects one cabinet at random and withdraws a transistor from one of the drawers.
a) What is the probability that an NPN transistor will be selected?
b) Given that the hobbyist selects an NPN transistor, what is the probability that it came from the cabinet that contains both types?
c) Given that an NPN transistor is selected what is the probability that it comes from the cabinet that contains only NPN transistors?

Answer 1

a) 0.5 = 50% probability that an NPN transistor will be selected.

b) 0.3333 = 33.33% probability that it came from the cabinet that contains both types

c) 66.67% probability that it comes from the cabinet that contains only NPN transistors

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

a) What is the probability that an NPN transistor will be selected?

1/3 probability that the first cabinet is chosen. This cabinet has two transistors, both of which are NPN, so 100% probability of selecting a NPN transistor.

1/3 probability that the second cabinet is chosen. This cabinet has two transistors, both of which are PNP, so 0% probability of selecting a NPN transistor.

1/3 probability that the second cabinet is chosen. This cabinet has two transistors, one of which is NPN, so 50% probability of selecting a NPN transistor.

So

`p = (1)/(3)*1 + (1)/(3)*0 + (1)/(3)*0.5 = (1)/(3) + (1)/(6) = (2)/(6) + (1)/(6) = (3)/(6) = 0.5`

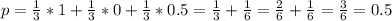
0.5 = 50% probability that an NPN transistor will be selected.

b) Given that the hobbyist selects an NPN transistor, what is the probability that it came from the cabinet that contains both types?

Here we use the conditional probability formula.

Event A: NPN transistor

Event B: From the third cabinet.

50% probability that an NPN transistor will be selected, so
`P(A) = 0.5`.

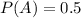1/6 probability that it is from the third cabinet and NPN, so
`P(A \cap B) = (1)/(6)`

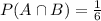
The desired probability is:

`P(B|A) = ((1)/(6))/(0.5) = 0.3333`

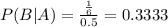
0.3333 = 33.33% probability that it came from the cabinet that contains both types.

c) Given that an NPN transistor is selected what is the probability that it comes from the cabinet that contains only NPN transistors?

Either it comes from the cabinet with only NPN transistors, or it comes from the cabinet with both types of transistors. The sum of the probabilities of these outcomes is 100%. So

x + 33.33 = 100

x = 66.67

66.67% probability that it comes from the cabinet that contains only NPN transistors