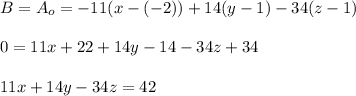Question

1. Find symmetric equations for the line that passes through the point

(4, −4, 8) and is parallel to the vector −1, 4, −3

(b) Find the points in which the required line in part (a) intersects the coordinate planes.
point of intersection with xy-plane

point of intersection with yz-plane

point of intersection with xz-plane

2. Find an equation for the plane consisting of all points that are equidistant from the points

(−6, 4, 1) and (2, 6, 5).

3. Find an equation of the plane.

The plane that passes through the point (−2, 1, 1) and contains the line of intersection of the planes

x + y − z = 3 and 4x − y + 5z = 5

Answer 1

The answer is below

Explanation:

1

a) The symmetric equations for the line that passes through the point (a, b, c) and is parallel to the vector (e, f, g) is:

`(x-a)/(e)=(y-b)/(f) =(z-c)/(g)`

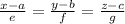
Therefore using the above equation to Find symmetric equations for the line that passes through the point (4, −4, 8) and is parallel to the vector (−1, 4, −3) we get:

`(x-4)/(-1)=(y-(-4))/(4)=(z-8)/(-3) \\\\Therefore:\\\\(x-4)/(-1)=(y+4)/(4)=(z-8)/(-3)`

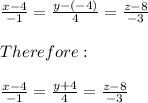
b)i) The line would intersect the xy plane where z = 0. Hence:

`(x-4)/(-1)=(y+4)/(4)=(0-8)/(-3)\\\\(x-4)/(-1)=(y+4)/(4)=(8)/(3) \\\\(x-4)/(-1)=(8)/(3)\ and\ (y+4)/(4)=(8)/(3)\\\\x=(4)/(3)\ and\ y=(20)/(3) \\\\Therefore\ the\ line\ intersect\ the\ xy\ plane\ at\ ((4)/(3),(20)/(3),0)`

ii) The line would intersect the yz plane where x = 0. Hence:

`(0-4)/(-1)=(y+4)/(4)=(z-8)/(-3)\\\\(y+4)/(4)=(z-8)/(-3)=4\\\\(y+4)/(4)=4\ and\ (z-8)/(-3)=4\\\\y=12\ and\ z=-4 \\\\Therefore\ the\ line\ intersect\ the\ yz\ plane\ at\ (0,12,-4)`

iii) The line would intersect the xz plane where y = 0. Hence:

`(x-4)/(-1)=(0+4)/(4)=(z-8)/(-3)\\\\(x-4)/(-1)=(z-8)/(-3)=1\\\\(x-4)/(-1)=1\ and\ (z-8)/(-3)=1\\\\x=3\ and\ z=5 \\\\Therefore\ the\ line\ intersect\ the\ xz\ plane\ at\ (3,0,5)`

2)

Let the points be A(−6, 4, 1) and B(2, 6, 5). Let O be the midpoint of the two points A and B. Therefore O is the average of the x coordinates, y coordinates and z coordinate.

`0=(1)/(2) (-6+2,4+6,1+5)=(- 2,5,3)\\\\`

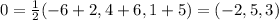
The normal vector (n) in the direction of line between A and B is:

n = AB = B - A = (2, 6, 5) - (−6, 4, 1) = (8, 2, 4)

n = 8x + 2y + 4z

The equation of the plane based on the normal vector and the midpoint 0 is:

Plane = 8x + 2y + 4z = 8(-2) + 2(5) + 4(3) = 6

Therefore:

8x + 2y + 4z = 6

4x + y + 2z = 3

3) The normal vectors to the plane are:

`n_1=(1,1,-1)\ and\ n_2=(4.-1,5)`

The point of intersection O of the two planes is normal to the normal vectors, hence:

`O=n_1*n_2=(1,1,-1)*(4,-1,5)\\\\O=(4, -9, -5)`

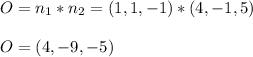
A point that lies on both plane is gotten by substituting z = 0, hence:

x + y - (0) = 3, and 4x - y + 5(0) = 5

x + y = 3 and 4x - y = 5

Solving simultaneously gives x = 8/5, y=7/5

From this two points we get:

AB = (-2-8/5, 1 - 7/5, 1-0) = (-18/5, -2/5, 1)

The vector normal to the plane (n) = (4, -9, -5) * (-18/5, -2/5, 1) = (-11, 14, -34)

`B=A_o=-11(x-(-2))+14(y-1)-34(z-1)\\\\0=11x+22+14y-14-34z+34\\\\11x+14y-34z =42\\`