Answer:
The population density for the village and the estate together is 112.5 people per square kilometer.
Step-by-step explanation:
The statement is incorrectly written. Correct form is described below:
A village has an area of 6 square kilometers and a population density of 600 people per square kilometer. An estate stituated next to the village has a population of 800 and a population density of 400 people per square kilometer. Work out the population density, in people per square kilometer, for the village and the state together.
Dimensionally speaking, the population density of the village and the estate together (
 ), measured in people per square kilometer, is defined by this expression:
), measured in people per square kilometer, is defined by this expression:
 (1)
(1)
Where:
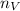 ,
,
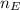 - Population of the village and the estate, measured in people.
- Population of the village and the estate, measured in people.
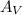 ,
,
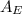 - Area of the village and the estate, measured in square kilometers.
- Area of the village and the estate, measured in square kilometers.
First, we find the population of the village:
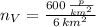
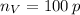
Then, we determine the area of the estate:

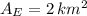
If we know that
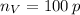 ,
,
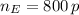 ,
,
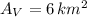 and
and
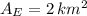 , then the population density of the village and the estate together is:
, then the population density of the village and the estate together is:
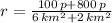
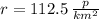
The population density for the village and the estate together is 112.5 people per square kilometer.