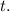Final Answer:
The derivative of
 is:
is:
![\[\mathbf{T}'(t) = \frac{\mathbf{r}''(t) \lvert \mathbf{r}'(t) \rvert - \mathbf{r}'(t) \mathbf{r}''(t)}{(\lvert \mathbf{r}'(t) \rvert)^2}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bfj8tum617i6rmalb2ljwrios375vxxrth.png)
Plugging in the expressions for
 and
and
 , we can find
, we can find
 . Finally, we can evaluate the curvature
. Finally, we can evaluate the curvature
 at the point
at the point
 by plugging in the appropriate value of
by plugging in the appropriate value of
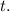
Explanation:
To find the curvature k of the curve at the point P, we can use the formula for curvature, which is given by:
![\[k = \frac{\lvert \mathbf{T}'(t) \rvert}{\lvert \mathbf{r}'(t) \rvert}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/aazxv468vhppt0h3caxvqpeeg4bqi1hbow.png)
where:
 is the vector-valued function that defines the curve, and
is the vector-valued function that defines the curve, and
 is the unit tangent vector.
is the unit tangent vector.
The prime notation
 denotes the derivative with respect to
denotes the derivative with respect to
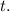
Given the vector-valued function
 we can first find the unit tangent vector
we can first find the unit tangent vector
 and its derivative
and its derivative
 Then we can evaluate the curvature at the point
Then we can evaluate the curvature at the point
 by plugging in the appropriate values of
by plugging in the appropriate values of
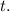
The unit tangent vector
 is given by:
is given by:
![\[\mathbf{T}(t) = \frac{\mathbf{r}'(t)}{\lvert \mathbf{r}'(t) \rvert}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/obgefrjjf7lvixjoqd05soyumfo0f1dcbo.png)
The derivative of
 is:
is:
![\[\mathbf{r}'(t) = e^t (-\sin(t) \mathbf{i} + \cos(t) \mathbf{j} + \sin(t) \mathbf{k}) + e^t \cos(t) \mathbf{i} + e^t \sin(t) \mathbf{j} + e^t \mathbf{k}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yuyk3b35wtp60qbmetia7hdqzz2vjw24jg.png)
![\[= e^t \cos(t) \mathbf{i} + e^t \sin(t) \mathbf{j} + (e^t - e^t \sin(t)) \mathbf{k}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/adgfdh8lr1kdxf0jvtas8a21fczq304e3l.png)
The magnitude of
 is:
is:
![\[\lvert \mathbf{r}'(t) \rvert = √((e^t \cos(t))^2 + (e^t \sin(t))^2 + (e^t - e^t \sin(t))^2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y1wc8k1ehey0a056ou4e9p6c95gr7jua8m.png)
![\[= \sqrt{e^(2t) (\cos^2(t) + \sin^2(t)) + e^(2t) - 2e^(2t) \sin(t) + e^(2t) \sin^2(t)}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ch39sxt0123sidwi6yhjb2w8zi8bcw9zs6.png)
![\[= \sqrt{e^(2t) + e^(2t) - 2e^(2t) \sin(t) + e^(2t) \sin^2(t)}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/swv4it1s4ucr448vchljdmxezkatek2dvo.png)
![\[= \sqrt{2e^(2t) - 2e^(2t) \sin(t)}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9rdynk8ksie6jqz7dm158ssp3t7lfrl867.png)
The unit tangent vector
 is then:
is then:
![\[\mathbf{T}(t) = \frac{e^t \cos(t) \mathbf{i} + e^t \sin(t) \mathbf{j} + (e^t - e^t \sin(t)) \mathbf{k}}{\sqrt{2e^(2t) - 2e^(2t) \sin(t)}}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/f34jjsklz9igcdi7e1p1fj45o0tx2pibyd.png)
The derivative of
 is:
is:
![\[\mathbf{T}'(t) = \frac{\mathbf{r}''(t) \lvert \mathbf{r}'(t) \rvert - \mathbf{r}'(t) \mathbf{r}''(t)}{(\lvert \mathbf{r}'(t) \rvert)^2}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bfj8tum617i6rmalb2ljwrios375vxxrth.png)
Plugging in the expressions for
 , we can find
, we can find
 Finally, we can evaluate the curvature
Finally, we can evaluate the curvature
 at the point
at the point
 by plugging in the appropriate value of
by plugging in the appropriate value of