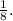The limit as
 approaches 0 for
approaches 0 for
 determined using
determined using
 Rule by taking the ratio of the derivatives of
Rule by taking the ratio of the derivatives of
 with respect to \(t\).
with respect to \(t\).
To find the limit
![\[\lim_{{t \to 0}} \frac{{v(t) - 3e^t}}{{2v(t) - 6}}\]](https://img.qammunity.org/2024/formulas/mathematics/college/ugw3rf01lkok4q6bgwzvdz3w5z1tjhgnk6.png)
we can use
 , which states that if the limit of the ratio of two functions
, which states that if the limit of the ratio of two functions
 as
as
 approaches a certain value is an indeterminate form (e.g., \( 0/0 \) or
approaches a certain value is an indeterminate form (e.g., \( 0/0 \) or
 then the limit of the ratio is the same as the limit of the ratio of their derivatives
then the limit of the ratio is the same as the limit of the ratio of their derivatives

First, let's find the derivatives of
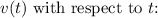
![\[ v'(t) = 4, \, 2.1, \, 0, \, 1.2, \, -3, \, -2, \, 1 \]](https://img.qammunity.org/2024/formulas/mathematics/college/m9is4xlxnc9l70504vxcd5008m0wvp7k3f.png)
Now, let's apply L'Hôpital's Rule to the given limit:
![\[\lim_{{t \to 0}} \frac{{v(t) - 3e^t}}{{2v(t) - 6}} = \lim_{{t \to 0}} \frac{{v'(t) - 3e^t}}{{2v'(t)}}\]](https://img.qammunity.org/2024/formulas/mathematics/college/6zol3fvogn6nwtct9lyb2hh1dj6hncorfu.png)
Substitute the values of
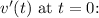
![\[= \frac{{4 - 3}}{{2 \cdot 4}} = (1)/(8)\]](https://img.qammunity.org/2024/formulas/mathematics/college/i9w25ni3rvsj203imu1svgfbkuksbi50je.png)
So, the limit is