Question

Help me pls... Thnx!

Answer 1

Given:

First term of a geometric series = a

Common ratio of the geometric series =
`√(3)`

To prove:

`S_(10)=121a(√(3)+1)`

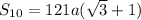
Solution:

The sum of first n terms of geometric series is

`S_n=(a(r^n-1))/(r-1)`

Where, a is the first term and r is the common ratio.

Putting n=10 and
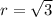`r=√(3)` in the above formula, to get the sum of 10 terms.

`S_(10)=(a((√(3))^(10)-1))/(√(3)-1)`

`S_(10)=(a(243-1))/(√(3)-1)`

`S_(10)=(242a)/(√(3)-1)`

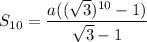
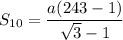
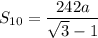
Rationalizing the denominator, we get

`S_(10)=(242a)/(√(3)-1)* (√(3)+1)/(√(3)+1)`

`S_(10)=(242a(√(3)+1))/((√(3))^2-1^2)`

`S_(10)=(242a(√(3)+1))/(3-1)`

`S_(10)=(242a(√(3)+1))/(2)`

`S_(10)=121a(√(3)+1)`

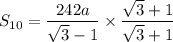
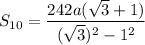
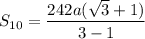
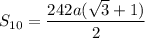
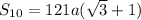
Hence proved.