Question

Kepler's third law indicates that the period (p) of an orbit is related to the semi-major axis (a) of the orbit with: p² = ka³. Kepler noticed that the value of the constant k changes when we observe systems with different central objects. This means that the orbits of all of the planets in the solar system have the same value for k, but that value is different for the moon because all of the planets orbit the sun, while the moon revolves around the Earth. Find the value of k for the planets using the Earth's orbit if Earth's orbital parameters are given as a = 1.50*10^11 m and p = 3.16 * 10^7 s.

Answer 1

To find the constant k for planets using Earth's orbit in Kepler's third law, we square Earth's orbital period and cube its semi-major axis, then divide the former by the latter. The value of k is approximately
`2.96 * 10^-19 s^2/m^3`, which applies to all planets orbiting the Sun.

Step-by-step explanation:

Finding Value of Constant k in Kepler's Third Law

To find the value of the constant k for the planets in our solar system using Earth's orbit, we apply Kepler's third law which states that the square of a planet's orbital period (P) is directly proportional to the cube of the semi-major axis (a) of its orbit. This relationship can be expressed by the formula:

`P2 = k * a3`

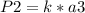
Given that Earth's semi-major axis is
`a = 1.50 * 1011` m and its orbital period is
`P = 3.16 * 107` s, we can solve for k as follows:

`P2 = (3.16 * 107 s)2 = 9.9856 * 1014 s2`

`a3 = (1.50 * 1011 m)3 = 3.375 * 1033 m3`

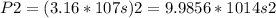
Now, we can calculate the value of k as:

`k = P2 / a3 = 9.9856 * 1014 s2 / 3.375 * 1033 m3`

`k ≈ 2.96 * 10-19 s2/m3`

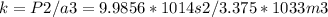
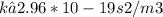
This value of k is specific to the Sun-Earth system and applies to all other planets orbiting the Sun.