Final answer:
To find the balloon's height with angles of elevation at 24.5 and 47.6 degrees and a horizontal distance of 8.4 miles between points on the ground, we use trigonometric functions in a system of equations involving these angles and tangent ratios.
Step-by-step explanation:
To determine how high a balloon is when it is 8.4 miles apart from two points on level ground, with angles of elevation of 24.5 degrees and 47.6 degrees to these two points, we can use trigonometry. We can imagine two right triangles sharing a common vertical side, which represents the height of the balloon, and we will use the tangent function, which relates the angles of elevation to the ratio of the vertical side opposite to the angle and the horizontal side adjacent to the angle.
Let's call the height of the balloon 'h', and the horizontal distances from the balloon to the points where the angles of elevation are measured 'd1' and 'd2' such that 'd1 + d2 = 8.4 miles'. Using the tangent of the given angles, we get two equations:
tan(24.5°) = h / d1
tan(47.6°) = h / d2
These can be rewritten as:
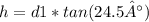
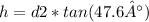
Because the height 'h' is the same for both equations, we can set them equal to each other and solve for one of the distances (either d1 or d2), then use that to find 'h'.
Step-by-step solution:
Solve for d1 or d2 using d1 + d2 = 8.4 miles
Substitute d1 or d2 into one of the tangent equations
Calculate 'h'
This calculation will give us the elevation of the balloon.