Question

What is the ideal speed to take a 100 m radius curve banked at a 20.0º angle?

Answer 1

The ideal speed to take a 100 m radius curve banked at a 20.0° angle can be found using the formula
`v = √(rg tan(θ))`, where r is the radius of the curve, g is the acceleration due to gravity, and θ is the banking angle. By inserting the given values and calculating the expression, the ideal speed can be determined.

Step-by-step explanation:

Ideal Speed for a Banked Curve

To find the ideal speed to take a 100 m radius curve banked at a 20.0° angle, we can use the concept of centripetal force and its relation to the gravitational force on the object moving along the banked curve. In an ideal scenario, where no friction is accounted for, the centripetal force required to keep the vehicle on a curved path is provided by the component of the gravitational force parallel to the road surface. The formula to calculate the ideal speed (v) for a banked curve is given by:

`v = √(rg tan(θ))`

Where r is the radius of the curve, g is the acceleration due to gravity (9.8 m/s²), and θ is the banking angle.

For a curve with a radius of 100 m and a banking angle of 20.0°, the ideal speed is calculated as follows:

`v = √(100 m × 9.8 m/s² × tan(20°))`

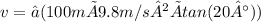
Upon calculating the above expression, the ideal speed for the curve can be determined.