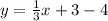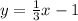Answer:
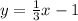
Step-by-step explanation:
Given
Parallel to:
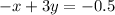
Passes through (-9,-4)
Required
Determine the line equation
First, we calculate the slope (m) of the said line
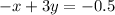
Make y the subject
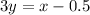
Divide through by 3
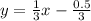
An equation has the general form:

Where
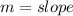
So:
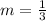
Because the required line is parallel to
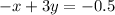 , then they have the same slope of
, then they have the same slope of
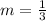
Next, is to calculate the line equation using:

Where
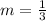
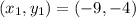
This gives:
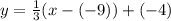
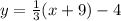
Open bracket