Question

Describe the relationship between __ and __ using geometric terms. What conjecture can you make about the midsegment of a triangle?

Answer 1

The midsegment of a triangle connects the midpoints of two sides, running parallel to the third side and equalling half its length. It is consistently shorter than either of the other two sides.

The midsegment of a triangle is a line segment that connects the midpoints of two sides of the triangle. Let's denote the midsegment as
`\( \overline{MN} \),` where
`\( M \) and \( N \)` are the midpoints of sides
`\( AB \) and \( AC \)` of the triangle
`\( ABC \),` respectively. Geometrically, the midsegment is parallel to the third side
`\( BC \)` and is half its length.

The relationship between the midsegment
`\( \overline{MN} \)` and the segment it connects
`(\( \overline{BC} \))` is characterized by parallelism and equality of lengths. This can be expressed using the parallel symbol
`(\( \parallel \))` and the equality symbol
`(\( = \))` as
`\( \overline{MN} \parallel \overline{BC} \) and \( \overline{MN} = (1)/(2)\overline{BC} \).`

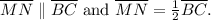
A conjecture that can be made about the midsegment of a triangle is that the midsegment is always shorter than either of the other two sides. This is a consequence of the midsegment being half the length of the third side. Symbolically,
`\( \overline{MN} < \overline{AB} \) and \( \overline{MN} < \overline{AC} \),`indicating that the midsegment is a median with the unique property of being the shortest segment among the three sides of the triangle. This conjecture holds true for any type of triangle, be it scalene, isosceles, or equilateral.

The probable question maybe:

Describe the relationship between the midsegment of a triangle and the segment it connects using geometric terms. What conjecture can you make about the midsegment of a triangle when it comes to its length compared to the lengths of the other two sides?