Question

A 5 kg block rests on a rough horizontal table. A rope is

attached to the block and is pulled with a force of 11N to the
left. As a result, the block accelerates at 2 m/s2. The coefficient
of kinetic friction between the block and the table is (round
to the nearest hundredth)

Answer 1

Approximately
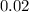`0.02` (assuming that
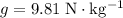`g = 9.81\; \rm N \cdot kg^(-1)`, and that the block was initially moving to the left.)

Step-by-step explanation:

Apply Newton's Second Law to find the net force on this block.

Mass of this block:
`m = 5\; \rm kg`.

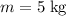Acceleration of this block:
`a = 2\; \rm m \cdot s^(-2)`.

`\begin{aligned}\text{Net force} &= m \cdot a \\ &= 5\; \rm kg * 2\; \rm m \cdot s^(-1) = 10\; \rm N\end{aligned}`.

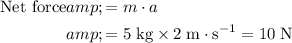The block is moving and accelerating towards the left. Hence, friction (which opposes motion) would be towards the right and would be opposite to the direction of the
`11\; \rm N` pulling force.

Therefore, the expression for the net force on this object would be:

`(\text{Net force} ) = (\text{Pulling force}) - (\text{Friction})`.

`10\; \rm N = 11\; \rm N - (\text{Friction})`.

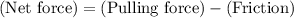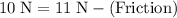Hence:

`\text{Friction} = 11\; \rm N - 10\; \rm N = 1\; \rm N`.

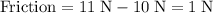The question states that this table is horizontal. Weight of the block (downwards) and normal force from the table (upwards) are the only two forces on this block in the vertical direction. Hence, the magnitude of the normal force on this block would equal to that of the weight of the block:

`\begin{aligned} |\text{Normal force}| &= |\text{Weight}| \\ &= m \cdot g \\ &= 5 \; \rm kg * 9.81\; \rm N \cdot kg^(-1) = 49.05\; \rm N\end{aligned}`.

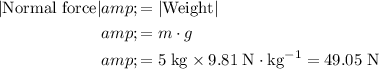Calculate the constant of kinetic friction between this block and the table:

`\begin{aligned}\mu_{\text{k}} &= \frac{\text{Friction}}{\text{Normal force}} \\ &= (1\; \rm N)/(49.05\; \rm N) \approx 0.02\end{aligned}`.