Question

A 166-g hockey puck is gliding across the ice at 24.5 m/s. A player whacks it with her stick, sending it moving at 39.1 m/s at 45.0∘ to its initial direction of motion.

What is the angle between the initial velocity of the puck and the force exerted on the puck?
If stick and puck are in contact for 136 ms, what is the magnitude of the average force that was exerted on the puck?

Answer 1

θ = 83.5º, F = 33.97 N

Step-by-step explanation:

For this exercise we use Newton's second law that the resultant of the external forces is in the direction of the acceleration, therefore we look for the force for each axis

the initial velocity is on the x axis v₀ₓ = 24.5 m / s

let's break down the final velocity

sin 45 = v_y / v

cos 45 = vₓ / v

v_y = v sin 45

vₓ = v cos 45

v_y = 39.1 sin 45 = 27.65 m / s

vₓ = 39, 1cos 45 = 27.65 m / s

now let's use the ratio of momentum and amount of movement, for each exercise

∫ F dt = Δp

X axis

Fₓ t =
`p_(fx) - p_(ox)`

Fₓ =
`m (v_(fx) - v_(ox) )/(t)`

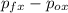
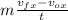
Fₓ = 166 10⁻³ (27.65 - 24.5) / 136 10⁻³

Fₓ = 3.84 N

Y axis

F_y t =
`p_(fy) - p_(oy)`

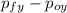
the initial velocity in the y axis is zero

F_y = m
`(v_(fy) )/(t)`

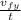
Fy = 166 10⁻³ 27.65 / 136 10⁻³

Fy = 33.75 N

Let's use the Pythagorean theorem to find the magnitude of the force

F =
`√(F_x^2 + F_y^2)`

F =
`√(3.84^2 +33.75^2)`

F = 33.97 N

the direction is found using trigonometry

tan θ = F_y / Fₓ

θ = tan⁻¹ F_y / Fₓ

θ = tan⁻¹ 33.75 / 3.84

θ = 83.5º