The pre-image XY obtained from the dilation of X'Y' with a scale factor of 2 from the center (0, 2) has endpoints at X(0, 14) and Y(0, 2). XY is twice the length of X'Y'.
The dilation involves a scale factor of 2 from the center (0, 2). To find the pre-image, you can apply the dilation to the endpoints of X'Y' to obtain XY. Let's calculate:
1. For point X' (0, 8):
- X will be at the same x-coordinate (0).
- Y will be
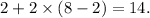
2. For point Y' (0, 2):
- X will be at the same x-coordinate (0).
- Y will be

So, the pre-image XY has endpoints located at X(0, 14) and Y(0, 2).
Now, let's compare the lengths of X'Y' and XY:
- The length of X'Y' is the vertical distance between the endpoints: 8 - 2 = 6.
- The length of XY is the vertical distance between the new endpoints: 14 - 2 = 12.
The correct statement is:
d. overline XY is located at X(0, 14) and Y(0, 2) and is twice the length of overline X'Y'.
The probable question may be:
Overline X'Y' has endpoints located at X'(0,8) and Y'(0,2) It was dilated at a scale factor of 2 from center (0,2). Which statement describes the pre-image?
a. overline XY is located at X(0,1) and Y(0,5) and is half the length of overline X'Y'
b. overline XY is located at X(0,1) and Y(0,5) and is twice the length of overline X'Y'
c. overline XY is located at X(0,5) and Y(0,2) and is half the length of overline X'Y'
d. overline XY is located at X(0,5) and Y(0,2) and is twice the length of overline X'Y'