Question

Maria has 64 meters of fencing to enclose a rectangular plot of land. She knows the area of the plot is 252 square meters. Find the dimension of Maria's plot of land.

Answer 1

18 meters by 14 meters

Explanation:

Area of rectangle is base times height (AKA length times width or however you wish to call the dimensions).

This question is a system of equations question. We can make two equations. We know that every rectangle must have 2 "lengths" and 2 "widths" (4 sides in a rectangle). Since Maria only has 64 meters of fencing, we get the equation:

2L+2W = 64

Now we know the area enclosed must be 252 so we have:

L* W = 252

Rewriting the second equation we get:
`W=(252)/(L)`

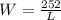
Plug this into first equation to get:
`2L+2\left((252)/(L)\right)=64`

`2L+(504)/(L)=64`

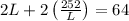
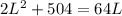`2L^2+504=64L` (multiply everything by L)

Solving the quadratic tells us L can be 18 or 14. Let's consider if L is 18 first by plugging 18 back into the second equation to get 18 * W = 252 which gives us W = 14. If we do the same for when L = 14, we get that W = 18.

Now you might wonder why we have 2 possible combinations, that's because in reality, it doesn't matter which one we label as length (L) or width (W).