Question

Which equation has the same solution as x, squared, minus, 12, x, minus, 12, equals, 7x

2
−12x−12=7

Answer 1

The equation
`\(y^2 - 19y - 12 = 0\)` has the same solution as
`\(x^2 - 12x - 12 = 7x\)`. The substitution y = x ensures that the solutions for y are equivalent to the solutions for x.

To find an equation with the same solution as
`\(x^2 - 12x - 12 = 7x\)`, we can start by moving all terms to one side of the equation:

`\[ x^2 - 12x - 12 - 7x = 0 \]`

Combine like terms:

`\[ x^2 - 19x - 12 = 0 \]`

Now, let's consider a different equation
`\(y^2 - 19y - 12 = 0\)`. By making the substitution y = x, the solutions to this equation will be the same as the solutions to the original equation. Therefore, the equation
`\(y^2 - 19y - 12 = 0\)` has the same solutions as
`\(x^2 - 12x - 12 = 7x\).`

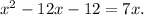
In summary, the equation
`\(y^2 - 19y - 12 = 0\)` has the same solution as
`\(x^2 - 12x - 12 = 7x\)`. The substitution y = x ensures that the solutions for y are equivalent to the solutions for x.

The probable question may be:

Write an equation which has the same solution as x, squared, minus, 12, x, minus, 12, equals, 7

x^2−12x−12=7