Question

Can someone answer part ABC

Answer 1

a) p for plain wrapping, h for holiday wrapping

b)
`\left \{ {{7p+4h=68} \atop {6p+2h=44}} \right.`

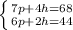
c) Plain wrapping paper cost $4/roll, and holiday wrapping paper costs $10/roll.

Explanation:

For part a, I've decided to with p for plain and h for holiday. Part b is somewhat simple;
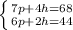`\left \{ {{7p+4h=68} \atop {6p+2h=44}} \right.` is the system we'll be using.

Now to do the actual work with part c.

I'll start by solving for p in 7p + 4h = 68.

7p + 4h = 68

Step 1: Subtract 4h from both sides.

7p = -4h + 68

Step 2: Divide both sides by 7/Multiply both sides by 1/7 (Either can be done)

p = 1/7(-4h + 68)

Step 3: Multiply 1/7 by -4h + 68

p = -4h/7 + 68/7

Now substitute -4h + 68/7 for p in the other equation (6p + 2h = 44).

6(-4h/7 + 68/7) + 2h = 44

Step 4: Multiply 6 by -4h/7 + 68/7.

-24h/7 + 408/7 + 2h = 44

Step 5: Add -24h/7 to 2h.

-10h/7 + 408/7 = 44

Step 6: Subtract 408/7 from both sides of the equation.

-10h/7 = -100/7

Step 7: Multiply both sides by -7/10, the reciprocal of -10/7.

h = 10

Now we know the holiday wrapping paper is $10/roll. Substitute 10 for h in p = -4h/7 + 68/7

p = 4(10)/7 + 68/7

Step 8: Multiply -4 by 10 to get -40.

p = -40/7 + 68/7

Step 9 (This is optional): Make what we have from Step 8 a single fraction.

p = (-40 + 68)/7

Steps 10 and 11: Add -40 and 68 to get 28, then divide that by 7 to get 4.

p = 4

And now we know the plain wrapping paper is $4/roll.

So, the complete sentence is: Plain wrapping paper cost $4/roll, and holiday wrapping paper costs $10/roll.