Question

Please..I'm desperate. I have a D in this class..

Find an equation of the tangent line to the curve at the given point. y = 6x - x^3, (1,5)​

Answer 1

Explanation:

Recall that the first derivative of an equation gives us the SLOPE for the tangent line.

So first, we should find the first derivative.

`(dy)/(dx) = 6 - 3x^2`

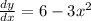
With the first derivative, we can solve for the SLOPE of the tangent line at (1,5).

Using x = 1.

`slope = 6 - 3(1)^2`

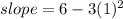
A tangent line is a line. And has the form
`y = mx +b`

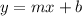
Where m is the SLOPE of the line. and b is the y-intercept.

To get to this equation, let's use the point-slope technique.

`y-y_1 = m(x-x_1)`

`y - 5 = m(x-1)`

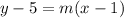
Solve for slope, substitute it into this equation for m and solve. That is the equation of the tangent line at the point (1,5).