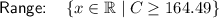Question

The daily production cost, C, for x units is modeled by the equation:

C = 200 - 7x + 0.345x^2
Explain how to find the domain and range of C.

Answer 1

The domain of the production cost function C = 200 - 7x + 0.345x^2 is all real numbers since there are no restrictions on the value of x.

,

The range of the production cost C is approximately from 173.61 to positive infinity. This is because the C function is a U-shaped quadratic function, and the minimum cost occurs at x ≈ 20.29, where the value of C is approximately 173.61. As x increases beyond this point, the cost continues to increase towards positive infinity.

Explanation:

To find the domain (valid values of x) for the given production cost equation C = 200 - 7x + 0.345x^2, there are no restrictions on the value of x. Therefore, the domain is all real numbers.

,

For the range (possible values of C), since the equation is a U-shaped quadratic function, the cost can take any value greater than or equal to its minimum point. To find the minimum point, we can use the formula x = -b / (2a), where a is the coefficient of the quadratic term and b is the coefficient of the linear term. In this case, the minimum point occurs at x ≈ 20.29.

,

By plugging this x-value back into the equation, we find the minimum cost C ≈ 173.61. Thus, the range of C is approximately from 173.61 to positive infinity.

Answer 2

`\textsf{Domain:} \quad \left\{x \in \mathbb{R}\; |\; x \geq 0\right\}`

`\textsf{Range:} \quad \left\{x \in \mathbb{R}\; |\; C \geq 164.49\right\}`

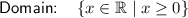
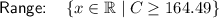
Explanation:

The daily production cost (C) for x units is modeled by the equation:

`C=200-7x+0.345x^2`

`\hrulefill`

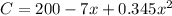
Domain

The domain of a function is the set of all possible input values (x-values) for which the function is defined.

In this case, since we cannot have a negative number of units, the domain is x ≥ 0.

Therefore, the domain of C is:

`\left\{x \in \mathbb{R}\; |\; x \geq 0\right\}`

`\hrulefill`

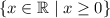
Range

The range of a function is the set of all possible output values (y-values) for which the function is defined.

The range of a quadratic equation with a positive leading coefficient is all values of y greater than or equal to the y-value of the vertex (minimum point).

The formula to find the x-value of the vertex of a quadratic equation in the form y = ax² + bx + c is:

`x = -(b)/(2a)`

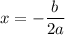
In this case, a = 0.345 and b = -7.

Therefore, the x-value of the vertex is:

`x = -((-7))/(2(0.345))=(7)/(0.69)=(700)/(69)`

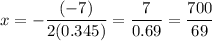
To find the y-value of the vertex, we can substitute x = 700/69 into the equation for C:

`C=200-7\left((700)/(69)\right)+0.345\left((700)/(69)\right)^2`

`C=(11350)/(69)`

`C\approx 164.49\; \sf (2\;d.p.)`

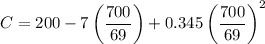
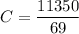
Therefore, the range of C is all values greater than or equal to 164.49:

`\textsf{Range:} \quad \left\{x \in \mathbb{R}\; |\; C \geq 164.49\right\}`