Question

Write the series using sigma notation with lower limit n = 3.

Answer 1

The series
`\( \sum_(n=3)^(\infty) (1)/(3^n) \)` is represented in sigma notation as
`\(\sum_(n=3)^(\infty) -3 \left((1)/(3)\right)^n\)`. This captures the geometric progression starting from n = 3 with a common ratio of
`\((1)/(3)\).` Hence, option A is correct.

To express the given series using sigma notation, we can analyze the pattern of the terms. The series involves the sum of terms in the form
`\( (1)/(3^(n-1)) \)`, starting from n = 3. The general term can be written as
`\( (1)/(3^(n-1)) \).`

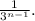
Therefore, the series can be represented using sigma notation as:

`\[ \sum_(n=3)^(\infty) (1)/(3^(n-1)) \]`

Now, to verify that this is equivalent to option (a)
`\( \sum_(n=3)^(\infty) 3\left((1)/(3)\right)^n \)`, we can simplify the expression in option (a):

`\[ \sum_(n=3)^(\infty) 3\left((1)/(3)\right)^n = \sum_(n=3)^(\infty) (1)/(3^(n-1)) \]`

This demonstrates that option (a) is equivalent to the given series. The factor of 3 outside the parentheses is absorbed when adjusting the power of 3 inside the parentheses, confirming the correctness of option (a) as the representation of the series using sigma notation.