Answer:
0.58 = 58% probability that the athlete is either a football player or a basketball player
Explanation:
We solve this question treating the probabilities as Venn's sets.
I am going to say that:
Event A: Athlete is a football player.
Event B: Athlete is a basketball player.
41% of the athletes are football players:
This means that
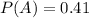
52% are basketball players
This means that
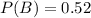
35% of the athletes play both football and basketball.
This means that
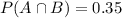
What is the probability that the athlete is either a football player or a basketball player
This is
 , which is given by the following equation:
, which is given by the following equation:
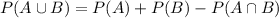 . So
. So
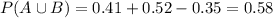
0.58 = 58% probability that the athlete is either a football player or a basketball player