As x approaches infinity, the functions f(x) that also approach infinity are (a)
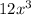 , (c)
, (c)
 , (e)
, (e)
 , and (f)
, and (f)
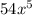 . These behaviors are determined by the leading terms in each function.
. These behaviors are determined by the leading terms in each function.
To determine which function approaches infinity as x approaches infinity, we can analyze the leading terms of each function, as they dominate the behavior for large values of x.
a.
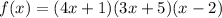
Leading term:
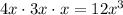
As x approaches infinity, f(x) also approaches infinity.
b.
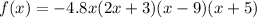
Leading term:
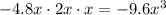
As x approaches infinity, f(x) approaches negative infinity.
c.
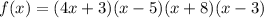
Leading term:
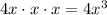
As x approaches infinity, f(x) also approaches infinity.
d.

Leading term:
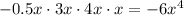
As x approaches infinity, f(x) approaches negative infinity.
e.
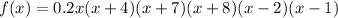
Leading term:
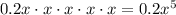
As x approaches infinity, f(x) also approaches infinity.
f.
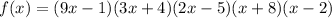
Leading term:
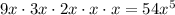
As x approaches infinity, f(x) also approaches infinity.
Therefore, the functions that approach infinity as x approaches infinity are: a, c, e and f.
The probable question may be:
As x approaches infinity, for which function does f(x) also approach infinity? Select all that apply.
Select all that apply:
a. f(x) = (4x + 1)(3x + 5)(x-2)
b. f(x)= -4.8x(2x+3)(x-9)(x+5)
c. f(x)= (4x+3)(x-5)(x+8)(x-3)
d. f(x)= -0.5x(3x-7)(4x + 1)(x+9)(x-3)
e. f(x)= 0.2x(x+4)(x+7)(x+8)(x-2)(x-1)
f. f(x) = (9x-1)(3x+4)(2x-5)(x+8)(x-2)