Question

Partially correct answer. Your answer is partially correct. Try again. Suppose that f left-parenthesis x right-parenthesis equals 1.5 x squared for negative 1 less-than x less-than 1. Determine the following probabilities: a) Upper P left-parenthesis 0 less-than Upper X right-parenthesis equalsEntry field with correct answer .5 b) Upper P left-parenthesis 0.5less-than Upper X right-parenthesis equalsEntry field with correct answer .4375 (Round the answer to 3 decimal places.) c) Upper P left-parenthesis negative 0.5 less-than-or-equal-to Upper X less-than-or-equal-to 0.5 right-parenthesis equalsEntry field with correct answer .125 (Round the answer to 3 decimal places.) d) Upper P left-parenthesis Upper X less-than negative 2 right-parenthesis equalsEntry field with correct answer 0 e) Upper P left-parenthesis Upper X less-than 0 or Upper X greater-than negative 0.5 right-parenthesis equalsEntry field with correct answer 1 f) Determine x such that Upper P left-parenthesis x less-than Upper X right-parenthesis equals 0.05. Entry field with incorrect answer .46415 (Round the answer to 3 decimal places.)

Answer 1

a. 0.5

b. 0.4375

c. 0.125

d. 0

e. 1

f. 0.9655

Solving

Explanation:

`given f(x)=\left \{ {{1.5x^(2) } \atop {0}} \right.\\`

for -1 ≤ x ≤ 1

a.

probability of P(0<X)

`\int\limits^1_0 {f(x) } \, dx \\x = 1.5x^(2) \\\int\limits^1_0 {1.5x^(2) } \, dx`

`1.5\int\limits^1_0 {x^(2) } \, dx`

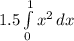
when we integrate we have

`1.5[x^(2+1) ]/3`

`= (1.5)/(3) \\= 0.5`

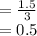
b. probability of 0.5<x<1

`=\int\limits^1_ {0.5} 1.5x^(2) \, dx`

`(7)/(16) = 0.4375`

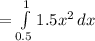
c. probability of p(-0.5≤X≤0.5)

I had difficulty using the math editor. ALmost ran out of time. please check the attachment for the solution to this.

the answer is 1/8 = 0.125

d. probability of x<-2 is equal to 0

e. p(x<0 or X>-0.5)

= p(X>-0.5) + p(x<0.5)

= 1-0.0625 + 0.0625

= 0.9375 + 0.0625

= 1

f.

we are to solve for P(x<X) = 0.05

= 0.9655

PLEASE CHECK ATTACHMENT FOR FULL CALCULATIONS