Question

Prove TM is a median without stating that the circumcenter of a right triangle is the midpoint of the hypotenuse.

Answer 1

In triangle RTS, with MN as the perpendicular bisector of TS and N as the midpoint, TM is proven as a median due to the midpoint property, perpendicular bisector property, and the resulting congruence of triangles TMN and NSM.

To prove that TM is a median in triangle RTS, we can use the midpoint property and the fact that MN is the perpendicular bisector of TS.

1. **Midpoint Property:** Since N is the midpoint of TS, it implies that TN = NS.

2. **Perpendicular Bisector Property:** MN is the perpendicular bisector of TS, meaning that MN bisects TS at a right angle.

Now, consider triangle TMN:

- TN = NS (midpoint property).

- MN is the perpendicular bisector of TS, so
`\(\angle TMN\)` and
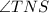`\(\angle TNS` are right angles.

By the Side-Angle-Side (SAS) congruence criterion, we can conclude that triangle TMN is congruent to triangle NSM.

Therefore, TM = SM.

Now, considering triangle TMS, we have TM = SM (just proved) and TS is common.

By the Converse of the Isosceles Triangle Theorem,
`\(\angle T\)` is congruent to
`\(\angle S\).`

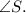
Since TM = SM and
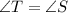`\(\angle T = \angle S\)`, we can now conclude that TM is a median in triangle RTS.