Question

A survey is conducted to determine the percentage of students at state universities who change their major at least once. In a SRS of 100 students 78% indicated that they graduated with a major different from the one with which they entered college. Determine a 95% confidence interval for the percentage of students who change their major.

Answer 1

95% confidence interval for the percentage of students who change their major

(0.69881 , 0.86119)

Explanation:

Step(i):-

Given that the sample size 'n' = 100

Given that the sample proprtion

p = 78% = 0.78

Level of significance =0.05

Critical value Z₀.₀₅ = 1.96

Step(ii):-

The 95% of confidence interval is determined by

`(p^(-) -Z_(0.05) (√(p(1-p)) )/(√(n) ) , p^(-) +Z_(0.05) (√(p(1-p)) ))/(√(n) ))`

`(0.78 - 1.96 (√(0.78(1-0.78)) )/(√(100) ) , 0.78 +1.96 (√(0.78(1-0.78) ))/(√(100) ))`

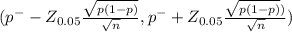
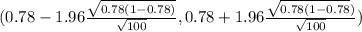
(0.78 - 0.08119,0.78 + 0.08119 )

(0.69881 , 0.86119)

Final answer:-

95% confidence interval for the percentage of students who change their major

(0.69881 , 0.86119)