Question

The number of typos made by a student follows Poisson distribution with the rate of 1.5 typos per page. Assume that the numbers of typos on different pages are independent. (a) Find the probability that there are at most 2 typos on a page. (b) Find the probability that there are exactly 10 typos in a 5-page paper. (c) Find the probability that there are exactly 2 typos on each page in a 5-page paper. (d) Find the probability that there is at least one page with no typos in a 5-page paper. (e) Find the probability that there are exactly two pages with no typos in a 5-page paper.

Answer 1

a) 0.8088 = 80.88% probability that there are at most 2 typos on a page.

b) 0.0858 = 8.58% probability that there are exactly 10 typos in a 5-page paper.

c) 0.001 = 0.1% probability that there are exactly 2 typos on each page in a 5-page paper.

d) 0.717 = 71.7% probability that there is at least one page with no typos in a 5-page paper.

e) 0.2334 = 23.34% probability that there are exactly two pages with no typos in a 5-page paper.

Explanation:

Poisson distribution:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

Binomial distribution:

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

The number of typos made by a student follows Poisson distribution with the rate of 1.5 typos per page.

This means that
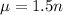`\mu = 1.5n`, in which n is the number of pages.

(a) Find the probability that there are at most 2 typos on a page.

One page, which means that
`\mu = 1.5`

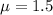
This is

`P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2)`

In which

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-1.5)*(1.5)^(0))/((0)!) = 0.2231`

`P(X = 1) = (e^(-1.5)*(1.5)^(1))/((1)!) = 0.3347`

`P(X = 2) = (e^(-1.5)*(1.5)^(2))/((2)!) = 0.2510`

`P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.2231 + 0.3347 + 0.2510 = 0.8088`

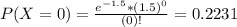
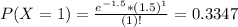
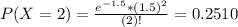
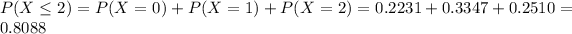
0.8088 = 80.88% probability that there are at most 2 typos on a page.

(b) Find the probability that there are exactly 10 typos in a 5-page paper.

5 pages, which means that
`n = 5, \mu = 5(1.5) = 7.5`.

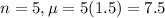This is P(X = 10). So

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 10) = (e^(-7.5)*(7.5)^(10))/((10)!) = 0.0858`

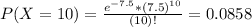
0.0858 = 8.58% probability that there are exactly 10 typos in a 5-page paper.

(c) Find the probability that there are exactly 2 typos on each page in a 5-page paper.

Two typos on a page: 0.2510 probability.

Two typos on each of the 5 pages: (0.251)^5 = 0.001

0.001 = 0.1% probability that there are exactly 2 typos on each page in a 5-page paper.

(d) Find the probability that there is at least one page with no typos in a 5-page paper.

0.2231 probability that a page has no typo, so 1 - 0.2231 = 0.7769 probability that there is at least one typo in a page.

(0.7769)^5 = 0.283 probability that every page has at least one typo.

1 - 0.283 = 0.717 probability that there is at least one page with no typos in a 5-page paper.

(e) Find the probability that there are exactly two pages with no typos in a 5-page paper.

Here, we use the binomial distribution.

0.2231 probability that a page has no typo, so
`p = 0.02231`

5 pages, so
`n = 5`

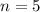
We want P(X = 2). So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 2) = C_(5,2).(0.2231)^(2).(0.7769)^(3) = 0.2334`

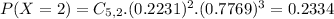
0.2334 = 23.34% probability that there are exactly two pages with no typos in a 5-page paper.