In a mathematical context, h(g(2)) is 6, f(h(x)) is
 . For given points and a table, f(g(2)) is -3/2, and g(f(5)) is 2. These computations involve function compositions and values from respective functions.
. For given points and a table, f(g(2)) is -3/2, and g(f(5)) is 2. These computations involve function compositions and values from respective functions.
Let's break down the given expressions step by step:
1. Given functions:
- f(x) = 5x
-
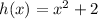
- g(x) = x - 4
a. h(g(2)):
![\[ h(g(2)) = h(2 - 4) = h(-2) = (-2)^2 + 2 = 6 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2rc5r7e03lyg1hf7ykd98at55qcljjf8gn.png)
b. f(h(x)):
![\[ f(h(x)) = f(x^2 + 2) = 5(x^2 + 2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cc0sza0udfvts97vfsfqiek6vzbqnb2zl1.png)
2. Given points for f(x) and the table for g(x):
f(x) points: (-2,2), (0,2), (3,4), (5,0), (6,-2), (8,-1)
g(x) table: x = -3, -1, 0, 2, 3, 5 and y = -5, -4, 2, 7, -1, 8
a. f(g(2)):
g(2) = 7.
Since there's no x = 7 in the graph, approximate using points (6, -2) and (8, -1):
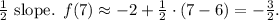
Therefore,
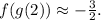
b. g(f(5)):
Find f(5) first using the coordinates for f(x) where x = 5 (the point (5,0)):
![\[ f(5) = 5 * 0 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/j4hz7pv7qeshignv9bzdc3exz3q006e62y.png)
Now, find g(f(5)):
g(f(5)) = g(0)
Use the table for g(x) where x = 0 (the point (0,2)):
g(0) = 2
Therefore, the answers are:
1. a. h(g(2)) = 6
b.
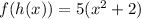
2. a. f(g(2)) = -3/2
b. g(f(5)) = 2