Question

Solve the following system of inequalities graphically on the set of axes below. State the coordinates of a point in the solution set. y≥-1/5x+5 y>2x-6

Answer 1

Solve the system of inequalities graphically:
`\(y \geq -(1)/(5)x + 5\)` and y > 2x - 6. On the graph, shade the overlapping region above the solid line and the dashed line. A point within this region, such as their intersection, belongs to the solution set.

To solve the system of inequalities graphically:

1. Graph each inequality separately:

- For
`\(y \geq -(1)/(5)x + 5\)`, draw a solid line with a slope of
`\(-(1)/(5)\)` and a y-intercept of 5. Shade the area above the line since it's
`\(y \geq\).`

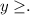
- For y > 2x - 6, draw a dashed line with a slope of 2 and a y-intercept of -6. Shade the area above the line since it's y >.

2. Identify the overlapping shaded region:

- The solution lies in the region where both shaded areas overlap.

3. Find a point in the solution set:

- Choose a point within the overlapping region. For example, the coordinates of the point where the two shaded regions overlap.